Kepler’s Laws
 |
The German mathematician and astronomer Johannes Kepler (1571 – 1630) was an avowed Platonist, and set out early in his professional career to demonstrate that the motion of the planets was circular, in accordance with the established Aristotelian doctrine, and that they could be described in terms of the Platonic solids (the crystal spheres). However, he was also a friend and assistant to the great Danish astronomer Tycho Brahe, who was making precise and detailed observations of the planets and stars. When Tycho Brahe died, in 1601, Kepler inherited this enormous mountain of raw data. After studying this data for 20 years, Kepler came to understand that his earlier assumptions about planetary motion had been naive, and that if an earth-centered (Ptolemaic) understanding of the universe were abandoned for a sun-centered (Copernican) model, then the motion of the planets was clearly elliptical. |
From this basis, Kepler generated his three famous “laws” of planetary motion:
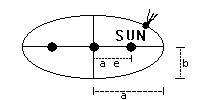
The First Law: The orbit of each planet is an ellipse with the sun at one focus (as shown below).
The Second Law: The line segment joining a planet to the sun sweeps out equal areas in equal time intervals (as shown below, left).
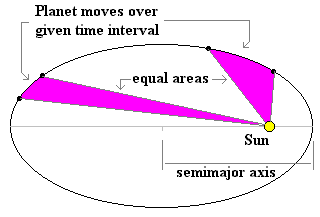

What the law describes is the observation that as a planet gets closer to the sun it moves faster, and as it moves more distant it moves slower (see animation at above right). It also means that two planets can have different eccentricity (e.g. perfect circle vs. elongated ellipse), but may still have the same orbital period if they have the same semimajor axis and the same focus (see animation below)

The Third Law: The square of the period of revolution of a planet about the sun is proportional to the cube of the semimajor axis of the planet’s elliptical orbit.
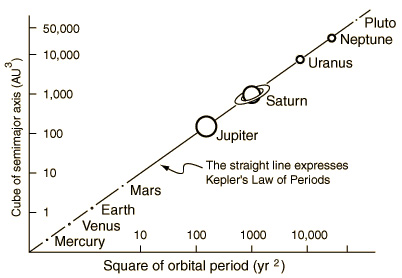
The third law means that if X is the length of a planet's year(orbital period), that is, the time it takes the planet to make a complete revolution about the sun, and if we denote by a the length of the semimajor axis of the planet’s orbit, then the quantity X2/a3 is the same for every planet (and comet, and other satellite) in the solar system. Thus, if a planet’s orbit is known, the length of it’s year can be immediately calculated, and vice versa.
Kepler’s laws were empirical, that is, they were derived strictly from careful observation and had no purely theoretical foundation. However, about 30 years after Kepler died, the English mathematician and physicist Sir Isaac Newton derived his inverse square law of gravity, which says that the force acting on two gravitating bodies is proportional to the product of their masses and inversely proportional to the square of the distance between them. Kepler’s laws may be derived from this theoretical principle using calculus.