
Edwin Hubble

Hubble, Edwin Powell 1889-1953
American astronomer whose observations proved that galaxies are "island
universes", not nebulae inside our own galaxy. His greatest discovery was the linear
relationship between a galaxy's distance and the speed with which it is moving (Hubble's
Law)..
In 1914 Vesto Slipher (lived 1870--1963) announced his results from the spectra of over 40 spiral galaxies (at his time people thought the ``spiral nebulae'' were inside the Milky Way). He found that over 90% of the spectra showed redshifts which meant that they were moving away from us. Edwin Hubble and Milton Humason found distances to the spiral nebulae. When Hubble plotted the redshift vs. the distance of the galaxies, he found a surprising relation: more distant galaxies are moving faster away from us. Hubble and Humason announced their result in 1931: the recession speed = H × distance, where H is a number now called the Hubble constant. This relation is called the Hubble Law and the Hubble constant is the slope of the line. The line goes through the origin (0,0) because that represents our home position (zero distance) and we are not moving away from ourselves (zero speed).
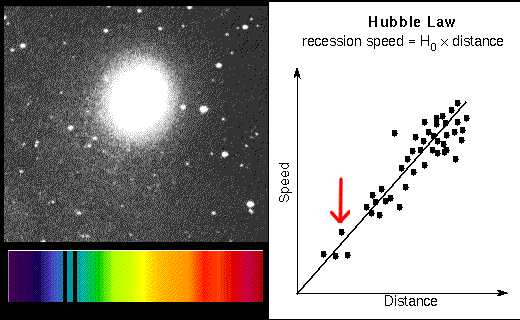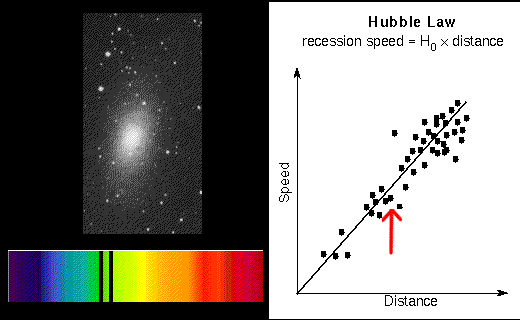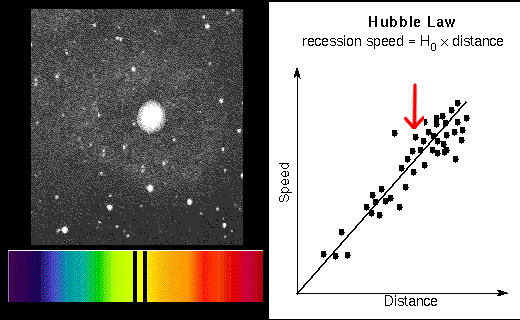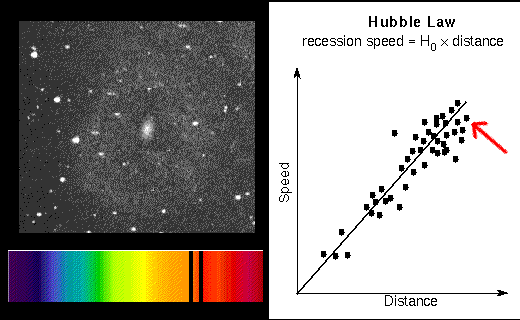
More distant galaxy has greater redshift.
If the distance is measured in units of megaparsecs (Mpc) and the recession speed is in kilometers/second (km/sec), the Hubble constant (slope of the line) is between 60 and 70 km/sec/Mpc. This value is found by using the galaxies that have accurate distances measured (Cepheids, etc.) and dividing their recession speeds by their distances. It is easy to find the recession speeds of galaxies from their redshifts. The Hubble law provides an easy way to measure the distances to even the farthest galaxies from the (recession speed/H). For example, if a galaxy has a redshift of 20,000 km/sec and H is set to 70 km/sec/Mpc, then the galaxy's distance = (20,000 km/sec)/(70 km/sec/Mpc) = 20,000/70 × [(km/sec)/(km/sec)] Mpc = 286 megaparsecs.